GameDev – Vector2D: Va chạm và phản xạ

Vector BounceĐể tính được hướng phản xạ của khi một vật thể va chạm vào mặt phẳng, ta có thể dựa vào góc nghiêng của mặt phẳng và vector theo từng vùng giá trị. Tuy nhiên cách tổng quát hơn là sử dụng các phép toán trên vector để thực hiện.

Xem Demo

Kiểm tra hai đoạn thẳng cắt nhau

Từ bài viết trước về tìm giao điểm của hai đường thẳng, ta có thể kiểm tra xem giao điểm tìm được có phải là giao điểm của hai đoạn thẳng hay không. Cách kiểm tra đơn giản là bạn xem điểm này có thuộc cả hai phần bao hình chữ nhật của hai đoạn thẳng. Tôi có phương thức kiểm tra như sau:

// detect if a point is inside the rectangle bound of this line
Line.prototype.insideRectBound = function(x, y){
	if(	Math.min(this.p1.x,this.p2.x) - x > EPSILON   ||
		x - Math.max(this.p1.x,this.p2.x) > EPSILON ||
		Math.min(this.p1.y,this.p2.y) - y > EPSILON ||
		y - Math.max(this.p1.y,this.p2.y) > EPSILON)
		return false;
	return true;
}

// ...
var intersected = _line1.insideRectBound(x,y) && _line2.insideRectBound(x,y);

Phương pháp

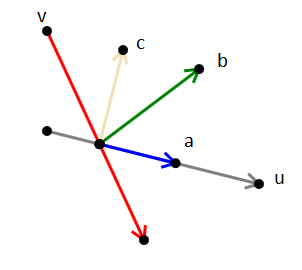Vector BounceTrong hình minh họa sau, vector v là hướng di chuyển của vật thể va chạm vào u. Vector phản xạ của v là b. Từ vector b ta phân tích ra hai vector thành phần là a và c (như vậy ta có a + c = b). Trong đó: a: vector chiếu của v trên u. c: vector chiếu của v trên đường thẳng vuông góc với u. Đây là vector pháp tuyến của u và có độ dài bằng khoảng cách từ gốc của v đến u. Như vậy để tìm được vector phản xạ b, ta chỉ cần theo 4 bước:

1. Tìm giao điểm của hai đoạn thẳng (tương ứng với hai vector v và u).

2. Tìm vector chiếu a của v trên u.

3. Tìm vector pháp tuyến của u có độ dài bằng khoảng cách từ gốc của v đến u.

4. Tính tổng vector a và c.

Xem mã nguồn minh họa bằng javascript sau để thấy chi tiết hơn:

<html>
<head>
  <script>
 /***************** Circle ***************/

function Circle(x,y) {
    this.x = x;
    this.y = y;
	this.radius = 5;
}

Circle.prototype.draw = function(context) {
    context.beginPath();
    context.fillStyle = "black";
    context.arc(this.x, this.y, this.radius, 0, Math.PI * 2, true);
    context.closePath();
    context.fill();
}
Circle.prototype.setPosition = function(x, y) {
    this.x = x + this.radius;
    this.y = y + this.radius;
}
Circle.prototype.contains = function(x, y) {
    var dx = this.x - x;
    var dy = this.y - y;

    return Math.sqrt(dx * dx + dy * dy) <= this.radius;
}

/***************** Line ***************/

function Line(x1,y1,x2,y2,color,hasHandles) {
    this.color = color;
	this.p1 = new Circle(x1,y1,5);
	this.p2 = new Circle(x2,y2,5);
	this.hasHandles = hasHandles;
}
Line.prototype.captureMouse = function(x,y) {
	if(this.p1.contains(x,y))
		return this.p1;
	if(this.p2.contains(x,y))
		return this.p2;
}
Line.prototype.getVector = function() {
	var x = this.p2.x-this.p1.x;
	var y = this.p2.y-this.p1.y;

	return {
		x: x,
		y: y,
		root: this.p1,
		length: Math.sqrt(x*x+y*y)
	};
}
// detect if a point is inside the rectangle bound of this line
Line.prototype.insideRectBound = function(x, y){
	if(	Math.min(this.p1.x,this.p2.x) - x > EPSILON   ||
		x - Math.max(this.p1.x,this.p2.x) > EPSILON ||
		Math.min(this.p1.y,this.p2.y) - y > EPSILON ||
		y - Math.max(this.p1.y,this.p2.y) > EPSILON)
		return false;
	return true;
}
Line.prototype.draw = function(context) {

	context.beginPath();
	context.strokeStyle = this.color;
	context.lineWidth = this.width;

	var headsize = 15;
    var angle = Math.atan2(this.p2.y-this.p1.y,this.p2.x-this.p1.x);
    context.moveTo(this.p1.x, this.p1.y);
    context.lineTo(this.p2.x, this.p2.y);
	context.lineTo(this.p2.x-headsize*Math.cos(angle-Math.PI/6),this.p2.y-headsize*Math.sin(angle-Math.PI/6));
    context.moveTo(this.p2.x, this.p2.y);
    context.lineTo(this.p2.x-headsize*Math.cos(angle+Math.PI/6),this.p2.y-headsize*Math.sin(angle+Math.PI/6));
	context.closePath();
	context.stroke();
	if(this.hasHandles){
		this.p1.draw(context);
		this.p2.draw(context);
	}
}
 /************** Main *************/
var EPSILON = 0.1;
var _canvas;
var _context;
var _movingShape = false;
var _line1, _line2, _line3, _line4, _line5;

function canvas_mousedown(e) {

    var x = e.pageX - _canvas.offsetLeft;
    var y = e.pageY - _canvas.offsetTop;

    _movingShape = _line1.captureMouse(x, y);
    if(!_movingShape)
		_movingShape = _line2.captureMouse(x, y);
}

function canvas_mousemove(e) {
	var x = e.pageX - _canvas.offsetLeft;
	var y = e.pageY - _canvas.offsetTop;

	if (_movingShape) {
        _movingShape.setPosition(x, y);
		update();
    }
}

function canvas_mouseup(e) {
    _movingShape = null;
}

function clear() {
    _context.clearRect(0, 0, _canvas.width, _canvas.height);
}
function findProjection(v1,v2){

	if(!v2.length)
		v2.length = Math.sqrt(v2.x*v2.x+v2.y*v2.y);
	// dot product
	var dp = v1.x*v2.x + v1.y*v2.y;
	// length of the projection of v1 on v2
	var length = dp/v2.length;

	// normalize vector v2
	v2.dx = v2.x/v2.length;
	v2.dy = v2.y/v2.length;
	// the projection vector of v1 on v2
	return {
		x: length*v2.dx,
		y: length*v2.dy,
	};

}
function update(){

	var a1 = (_line1.p2.y-_line1.p1.y)/(_line1.p2.x-_line1.p1.x);
	var b1 = _line1.p2.y - a1*_line1.p2.x;

	var a2 = (_line2.p2.y-_line2.p1.y)/(_line2.p2.x-_line2.p1.x);
	var b2 = _line2.p2.y - a2*_line2.p2.x;

	// find intersection point
	// y = a1x + b1
	// y = a2x + b2
	// a1x + b1 = a2x + b2
	// (a1 - a2)x = b2 - b1
	var x = (b2 - b1)/(a1 - a2);
	var y = a1*x+b1;

	var intersected = _line1.insideRectBound(x,y) && _line2.insideRectBound(x,y);

	var v1 = {
		x: x - _line1.p1.x,
		y: y - _line1.p1.y
	};

	var v2 = _line2.getVector();

	var v3 = findProjection(v1,v2);

	if(intersected)
	{
		_line3.p1.x = x;
		_line3.p1.y = y;
		_line3.p2.x = _line3.p1.x+v3.x;
		_line3.p2.y = _line3.p1.y+v3.y;

		// perpendicular vector of v2
		var v4 = {
			x: v2.y,
			y: -v2.x
		};

		v4 = findProjection(v1,v4);
		// bounce
		v4.x = -v4.x;
		v4.y = -v4.y;

		_line4.p1.x = x;
		_line4.p1.y = y;
		_line4.p2.x = x + v4.x;
		_line4.p2.y = y + v4.y;

		// bounce vector
		var v5 = {
			x: v3.x + v4.x,
			y: v3.y + v4.y
		};

		_line5.p1.x = x;
		_line5.p1.y = y;
		_line5.p2.x = x + v5.x;
		_line5.p2.y = y + v5.y;
	}

	// draw
	clear();

    _line1.draw(_context);
	_line2.draw(_context);

	if(intersected)
	{
		_line3.draw(_context);
		_line4.draw(_context);
		_line5.draw(_context);
	}

	_context.fillText(genFormula(a1,b1),10,20);
	_context.fillText(genFormula(a2,b2),10,40);

	_context.beginPath();
    _context.fillStyle = "yan";
    _context.arc(x, y, 5, 0, Math.PI * 2, true);
    _context.closePath();
    _context.fill();

}
function genFormula(a,b)
{
	a = floor(a);
	b = floor(b);
	var s = "y = ";
	if(a!=0)
		s += (a==1?"":a)+"x";
	if(b!=0)
		s += (b>0?(a==0?"":"+"):"")+b;
	return s;
}
function floor(number)
{
	return Math.floor(number*10)/10;
}

window.onload = function(){
	_canvas = document.getElementById("canvas");
	_context = _canvas.getContext("2d");
	_context.font = "16px Arial";
	_context.lineWidth = 3;

	_line1 = new Line(100, 100, 200, 250,"red",true);
	_line2 = new Line(100, 200, 300, 200,"gray",true);
	_line3 = new Line(100, 300, 300, 250,"blue",true);
	_line4 = new Line(100, 300, 400, 200,"wheat",true);
	_line5 = new Line(100, 300, 400, 200,"green",true);

	_canvas.onmousedown = canvas_mousedown;
	_canvas.onmousemove = canvas_mousemove;
	_canvas.onmouseup = canvas_mouseup;

	update();

}
  </script>
</head>
<body>
<canvas id="canvas" width="400px" height="400px" style="border: 1px solid"></canvas>
</body>
</html>

YinYang’s Blog

Bài này đã được đăng trong Algorithms, Game Dev, General, HTML5 - Canvas và được gắn thẻ , . Đánh dấu đường dẫn tĩnh.

3 bình luận về “GameDev – Vector2D: Va chạm và phản xạ”

Đã đóng bình luận.